The notion of sound is rather remarkable. Something happens there and we know it here, even if we are looking the other way, not paying attention, or even asleep. The fact that some sounds can produce physical and emotional effects is just short of astounding. These notes will perhaps remove some of the mystery associated with sound and hearing, but probably none of the wonder.
Sound is a disturbance of the atmosphere that human beings can hear. Such disturbances are produced by practically everything that moves, especially if it moves quickly or in a rapid and repetitive manner.
You should be aware that the air is made up of molecules. Most of the characteristics we expect of air are a result of the fact that these particular molecules are very light and are in extremely rapid but disorganized motion. This motion spreads the molecules out evenly, so that any part of an enclosed space has just as many molecules as any other. If a little extra volume were to be suddenly added to the enclosed space (say by moving a piston into a box), the molecules nearest the new volume would move into the recently created void, and all the others would move a little farther apart to keep the distribution even.
Because the motion of the molecules is so disorganized, this filling of the void takes more time than you might think, and the redistribution of the rest of the air molecules in the room takes even longer. If the room were ten feet across, the whole process might take 1/100 of a second or so.

If the piston were to move out suddenly, the volume of the room would be reduced and the reverse process would take place, again taking a hundredth of a second until everything was settled down. No matter how far or how quickly the piston is moved, it always takes the same time for the molecules to even out.
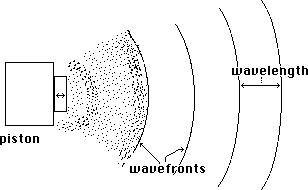
In other words, the disturbance caused by the piston moves at a constant rate through the air. If you could make the disturbance visible somehow, you would see it spreading spherically from the piston, like an expanding balloon. Because the process is so similar to what happens when you drop an apple into a bucket, we call the disturbance line the wavefront.
If the piston were to move in and out repetitively at a rate between 20 and 20,000 times a second, a series of evely spaced wavefronts would be produced, and we would hear a steady tone. (One wavefront is heard as a click.) The distance between wavefronts is called wavelength.
Under normal conditions a wavefront moves through air at 1130 feet per second. This is the speed of sound .
I mentioned that air gets its properties from the weight and speed of its molecules. Molecules of different weight (other gases maybe) or different velocity (that translates into temperature) will exhibit different speeds of sound. Motion of the sound source, the listener, or the air itself has no effect on the speed of sound, nor does the pressure of the air.
An impulse applies a chunk of energy to the air. (This energy becomes a difference in pressure before and behind the wavefront.) As the front expands, the energy is spread over a larger and larger area, in a way suggested by the relationship between the radius and area of a sphere, A=4¼r^2. The total energy stays the same, the area expands, so the energy in one unit of area decreases with the square of the distance from the source. The front will continue moving until there isn't enough energy to measure. The stronger the impulse, the farther the wavefront goes (the sound of the explosion of the volcano Krakatoa is said to have gone around the world three or four times).
When sound hits something soft or movable the energy of the wavefront is dissipated in moving the object around. If the object is rigid, like a wall, two things happen. Part of the energy of the wavefront will set up a wavefront within the wall; just how big a part is transmitted this way depends on the material the wall is made of. The rest of the energy is reflected off the surface according to the same rules that apply to light on a mirror. (The most important of these is that "the angle of reflection equals the angle of incidence".)
Here's what happens in two kinds of situations, one in which the source of disturbance is relatively close to the wall, and one in which the source is far enough away that you don't notice the wavefront is curved. Several repeated wavefronts are shown in each example.
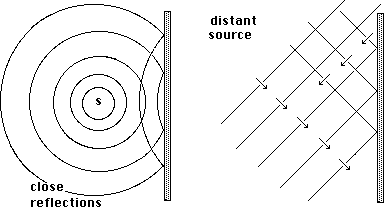
At the risk of getting ahead of myself, I will point out two important effects of reflections. One is that a listener might hear something twice if the distances involved are great enough, the other is that the energy reflected back into a room is going to change our notions about how long the disturbance endures.
When the wavefront hits a wall with a hole in it a small portion of the wave energy leaks through the hole and begins propagating as if the hole were the source, that is, spherically around the hole. The amount of energy available depends on the size of the hole. This process is known as diffraction.
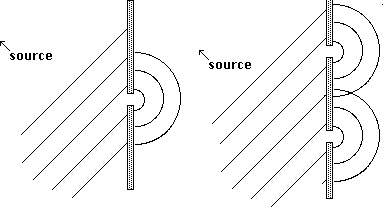
An interesting effect is created when there are two holes in the wall. Each hole produces a wavefront, and the two separate wavefronts coincide at some point. If you happened to measure the strength of the wave at that point, the energies of both fronts would be combined, and the measurement would be quite different from one obtained only a few inches away. This effect is called interference .
Now let's backtrack and see what happens when we produce a lot of wavefronts at a steady rate. Initially, the separate fronts do not interact because each moves away from the source at the same speed. If we could freeze everything and take some measurements, we would see that the wavelength was a distance expected by considering the rate of repetition and the speed of sound. While things were still frozen, we could make a graph of the exact pressure changes in the space between the wavefronts. We call that graph the waveform . (Since the repeating waves are created by something moving back and forth, the waveform will represent a pressure pattern that goes both above and below the "normal" or undisturbed value.)
I should take this opportunity to point out that the time between the creation of wavefronts is called the period , and that the number of waves produced per second is called the frequency . (Events per second is such a common concept in acoustics it needs an abbreviation. For a long time cps was used, but that can be confused with some other units so the name was changed to Hertz, abbreviated Hz. Sound frequency is often in the thousands, so we might refer to kiloHertz, (kHz) when we mean 1000 Hz.)
Now, letting our waves move again, we find the behavior of repeating wavefronts is the same as for those taken one at a time, but complications can arise.
For instance, I said that the movement of the wave through the air is not affected by any motion of the source or listener. However, motion will affect measurements of wavelength or frequency of repeating waves. If the source were to move toward you between production of wavefronts, it would seem to be chasing the first front, and the second front would be a little closer to the first than you would expect.
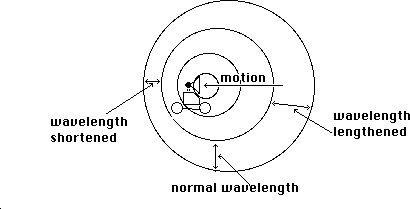
If you from, behind the source, the wavefronts would be too far apart. If you measure at right angles to the motion, you would get the "right" answers. Similarly, any measurement of frequency would be high in the direction of movement, and low behind the source. This is called the doppler effect , and works the same way if the measuring apparatus is moving and the source standing still.
When you analyze reflection and diffraction of repeating waves, you have the complication of waves running into each other. Now when two waves intersect, they have absolutely no effect on each other, but if you happen to measure the pressure at that particular point and time, you find the pressures of the two waves added together. If the two low spots coincide, you get a super low reading, and if the high of one wave coincides with the low of the other, you might easily get the normal value for the room and conclude nothing was going on at all.
You might think these are only momentary aberrations, but in fact it is quite easy for reflection or diffraction to establish locations where there will always be coinciding waves which are matched up high for high and low for low. (In phase.) These locations are any spot where two waves will pass, and for which one wave must travel exactly one wavelength (or multiple thereof) farther than the other one to reach. At this spot the two waves reinforce each other.
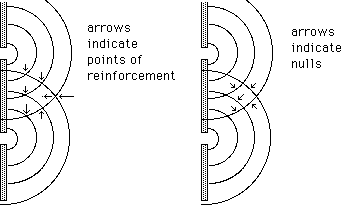
It also is common to find spots where two intersecting waves are matched up high for low and low for high (out of phase). Such spots are anywhere that two waves must pass where one of the waves will travel one half (or 1+1/2, or 2+1/2 etc.) wavelength farther than the other. At this spot, the two waves cancel each other out.
If you study the drawing, you can find many places where the two sets of waves produced by the holes are in phase and, not far away, spots where the waves are out of phase. You should also realize that if the wavelength were to be changed, the in-phase and out-of-phase spots would move. Notice that as you move away from the holes, you find fewer such spots, so that at a distance of four or five wavelengths you are safe from this phenomenon. This whole effect, incidentally, is produced by any obstacle with a size equal to or larger than the wavelength. (This is called "shadowing", although we don't get reduced sound in the shadow, merely these interference effects.)
This drawing shows how an extreme case of reinforcement can be established.It happens when the sound originates between two parallel surfaces such as the walls of a shower stall.
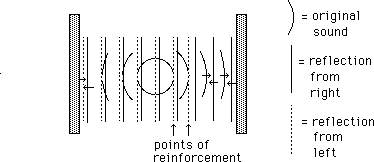
Here, the parallel walls happen to be exactly nine wavelengths apart. A wave will bounce off the right wall, travel to the left wall and bounce again, arriving at the source in phase with the new wavefronts. If the walls are fairly reflective, a particular front will pass many times, so the pressure differences measured at the points of reinforcement will be the sum of several waves. This will make the magic pitch really boom out.
This process is very dependent on the wavelength of the sound, and therefore the frequency. Change it only slightly and the system will settle down, double it or cut it in half and things go wild again. Standing waves are a pain in the neck in rooms, but can be very useful in the construction of musical instruments.
Peter Elsea Nov, 1995