
The Numbers (and Initials) of Acoustics
Architectural acoustics is about half engineering, half art. The art comes from experience in choosing, placing and evaluating various materials and structures. The engineering comes from measuring the effects of the materials and structures and relating what can be measured to what can be heard. There are standards for making test measurements so you can compare specifications from various manufacturers when choosing materials and prebuilt items such as doors. The standards are also used in specifying and evaluating performance of finished construction such as floor, wall, and window isolation.
Graphs
Many acoustical numbers are presented as curves on graphs. In order to accommodate the nature of hearing, peculiar graph paper is often used. The horizontal divisions represent frequency, but they are spaced in such a way that an octave is the same width anywhere across the graph. Notice that each mark up to 100 represents 10 hz, each from 100 to 1000 represents 100hz, and from 1000 to 10,000, each is 1000 hz. The spacing is therefore logarithmic. The vertical divisions are equally spaced, but since they are marked in decibels, the graph is logarithmic in this direction also. This makes the perceived effect of any deviations in the curves the same anywhere on the graph.

Fig 1 Logarithmic graph paper
Equal Loudness Curves
You will see lots of references to equal loudness curves or equal loudness contours- these are based on the work of Fletcher and Munson at Bell labs in the 30s, or perhaps refinements made more recently by Robinson and Dadson. These were made by asking people to judge when pure tones of two different frequencies were the same loudness. This is a very difficult judgement to make, and the curves are the average results from many subjects, so they should be considered general indicators rather than a prescription as to what a single individual might hear.
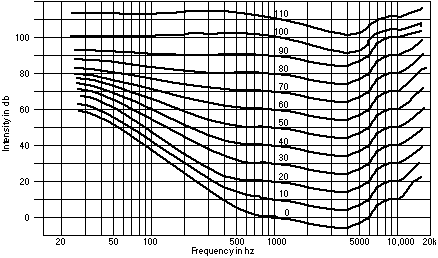
Fig 2. Equal loudness contours or Fletcher-Munson curves
The numbers on each curve identify it in terms of phons, a unit of loudness that compensates for frequency effects. To find the phon value of an intensity measurement, find the db reading and frequency on the graph, then see which curve it lands on.
The interesting aspects of these curves are that it is difficult to hear low frequency of soft sounds, and that the ear is extra sensitive between 1 and 6 kilohertz.
SPL
Sound Pressure Level is a single measurement of sound pressure in decibels relative to the threshold of hearing. That varies from person to person of course, but for the purposes of SPL measurements is defined as 2 X 10-5 Newtons per Meter2 or 20 microPascals. We generally live in the mid 60s dbSPL, think music is loud when it gets above 90 dbSPL, and complain of pain at 120 dbSPL .
When SPL measurements are made, some adjustment for the ear's response to low frequency is usually included. This is done by using filters that follow the Fletcher-Munson curves - the A curve follows F&M at low levels and the B curve follows intermediate levels. The C curve is nearly flat.
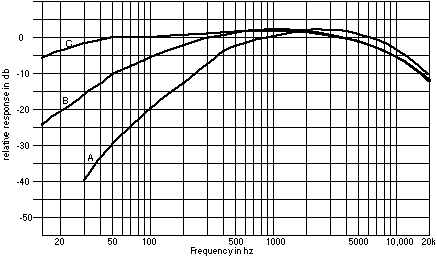
FIG.3 SPL Weighting curves,
If it seems odd that these curves turn down when the equal loudness curves turn up, remember that this is a frequency response and the loudness curve indicates sensitivity. The idea is that if you find noise at a low level and low frequency, it doesn't count for much since it is hard to hear.
SPL is usually measured with special meters that have the weighting curves built in. Use the A curve for soft measurements and the C curve for loud sounds, and the flat setting for comparative measurements like transmission loss.
NC
Noise Criteria levels or NC ratings are a common way of specifying the background noise in rooms. It's not quite the same as SPL- there is a special filter used which discounts low frequency sound even more. It also only includes about half of the audible spectrum. Generally, A weighted SPL readings run about 10db higher than NC readings.
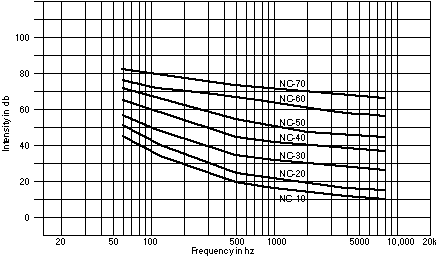
Fig. 4 Noise Criteria curves
To get an NC value, find the curve that is just below all of your measurements. You can see from these curves that an environment that measures NC-20 could have a 50 db level of 60hz hum. Although the Fletcher-Munson effect would make this tolerable for a classroom, it's not appropriate for a recording studio, because soft sounds are often amplified to the point where our hearing response is flat.
TL
Transmission Loss is simply the reduction of SPL as sound travels through a structure. It will vary with frequency, and should be presented as a curve or series of numbers at selected frequencies. Very often you see a chart like this:
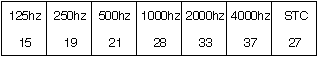
Fig 5. Transmission loss
This gives the transmission loss in db at the frequencies listed. Notice the last entry, instead of a frequency, is an overall rating called STC.
STC
Sound Transmission Class is another set of curves, again relaxed in stringency at low frequency. To convert a TL curve to STC, you find an STC curve that fits the measured curve within 8 db, then specify the value from the STC curve at 500hz. This is useful for comparing products in a catalog, but the true transmission loss curve is necessary to predict what will happen with music.
Absorption Coefficient
The absorptive efficiency of a material is given by its Absorption Coefficient, which is the ratio of the sound energy that is reflected back to the arriving sound energy. A totally reflective material has an absorption coefficient of 0, and an open window has an AC of 1. As with most things acoustical, the value varies with frequency, although you will often see a single number specified. Here's how various thicknesses of Fiberglas stack up:
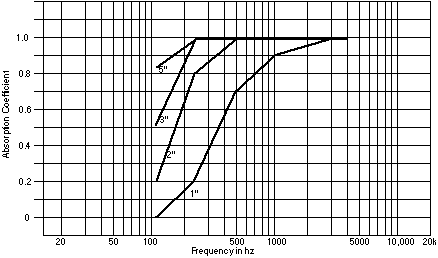
Figure 6. Absorption Coefficient of Fiberglas.
NRC
The Noise Reduction Coefficient of a material is the average absorption measured at 250, 500, 1000, and 2000 hz. It's useful for designing offices, but not sound studios. Even the complete specs given above don't tell what happens in the lowest octaves, although you can guess from the trend of the curves.
Speed of Sound
The most important number to remember is that the speed of sound under typical conditions is 1130 ft/second. This varies with temperature (slows down when it's cold) but not with any other conditions you will encounter in recording studios. For many purposes, we can use the rule of thumb that sound travels a little faster than one foot in a millisecond.
Frequency
This how often something happens. For a steady tone, the frequency is the number of wavefronts that pass your ear in one second. It is measured in hertz or hz, which can be though of as meaning 1/sec or "per second". We usually consider the audible range of frequency to be from 20hz, to 20,000hz. Few people can hear all of this range, but some can hear beyond.
Wavelength
This is the distance between wavefronts of a steady tone. It is often represented in formulas by the greek letter lambda, which looks like an upside down y.
The formula.
Remember the relationship between frequency, wavelength and speed of sound is:
Wavelength = Speed_of_Sound / Frequency