Room Modes
Your basic rectangular room is going to encourage certain frequencies with wavelengths that are related to the dimensions of the room. There are two mechanisms at work here. In rooms with highly reflective walls, the sound pressure wave along certain paths may return to the origin of the wave just in time to reinforce the next cycle of pressure. This sets up a standing wave or flutter echo. It is also possible for the room as a whole to resonate in a manner similar to a struck drum. In both cases, the intensity of sound will vary according to frequency as you move around a room. You can test this two ways- play a steady tone and move around the room (often all you need do is turn your head) or sweep the frequency of the tone and note the slight differences in loudness.
Calculation by Geometry
The two mechanisms are examined by different methods. High frequency waves can be analyzed by assuming the sound behaves like a ray-- traveling in a straight line and reflecting off of surfaces at an angle equal to the incidence. We can calculate the fundamental frequency of the wave by examining the geometry of the room. The actual effects depend on the size and reverb time of the room, but are generally limited to frequencies above the fifth harmonic.
Axial Modes
The simplest path is the round trip between two opposing surfaces in the room. We can calculate the fundamental frequency for this effect using the formula:
![]()
Where F = frequency, W = wavelength, and c = the speed of sound.
If we want to calculate the effect of an 8 foot ceiling, the wavelength is 2H or 16 ft. (Remember, it's a round trip.)
The speed of sound is 1130 ft/second, so the fundamental of enhanced frequencies is 70hz.
The same thing will happen for the length and width of the room. These three paths are called the axial modes.
Tangential Modes
Any closed path that includes four surfaces is tangential. A four bank shot that reflects from the center of each wall will have the same path length as the room diagonal. If the room is square, many tangential paths have the same length as the diagonal.
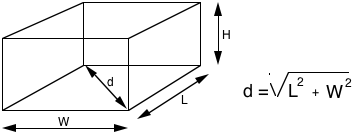
The wavelength can be figured from the length and width by the Pythagorean theorem.
There are more tangential modes, such as this one, seen from above:
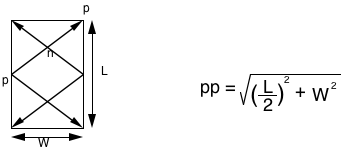
In this mode, you have two paths that support some standing wave action. At the intersection n (called a node) both waves come together. They will be exactly in phase, and the experience would be like a standing wave from p to p. The distance pp is calculated from the root of the squares of the width and half the length. (The other intersection would be called an antinode. Can you imagine why?)
Likewise, there are tangential modes involving one third the length, one half the width, and combinations of the above.
Oblique Modes
A mode that involves all six surfaces is oblique. The principal oblique mode runs along the grand diagonals from opposite corners such as left top front to right bottom rear.
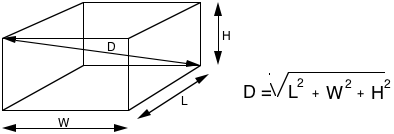
The diagonal is calculated from Pythagoras as before, but it's three dimensional now. There are more complex oblique modes I won't try to illustrate.
Sound waves only behave as rays when the wavelength is small compared to the surrounding structure. This is affected by the volume and reverb time of the room. You can work out the lower limit of frequency with the formula:
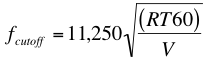
Waves at these frequencies are easily absorbed with material of manageable thickness, and the direct paths will often be broken up by furniture, so problems with these modes are seldom serious. These relationships are useful in the initial design of a room. The goal is to come up with a shape where none of the principal dimensions or diagonals match or are simply related. For instance a room with an 8 ft. ceiling and a 16 ft. wall would have extra problems with harmonics of 140 Hz.
Room Resonance
For Low frequency modes we need to investigate the resonance behavior of the room as a whole. This begins with the Rayleigh wave equation:
![]()
where
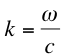
The p in this equation stands for pressure. After seven pages of industrial strength calculus, we arrive at a formula for determining the frequency of each resonance mode.
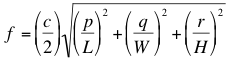
In this equation, p. q and r stand for wave numbers of the three axial modes. We then enter Width, Length, and height of the room, and the speed of sound for c, and solve with values of p, q, and r from this table:
|
P |
q |
r |
|
1 |
0 |
0 |
|
0 |
1 |
0 |
|
0 |
0 |
1 |
|
1 |
1 |
0 |
|
1 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
1 |
1 |
|
2 |
0 |
0 |
|
2 |
1 |
0 |
and so on until we have as many values as we have room for, usually for all combinations up to 4,4,4. Note that in the cases where two of the three wave numbers are 0, the formula yields the same frequencies seen in the geometric approach.
It is easy to set this up in a spreadsheet where the p q and r numbers are each in a column. The formula in the frequency column would look something like this:
= 565 *SQRT(POWER(B5,2)/POWER($E$1,2) + POWER(C5,2)/POWER($E$2,2) + POWER(D5,2)/POWER($E$3,2))
After we have the numbers, we sort them and look for clusters of modes and empty regions where there are no modes. Here's an example for a room in my house:
|
L |
|
|
|
15.08 |
|
W |
|
|
|
9.8 |
|
H |
|
|
|
8.33 |
|
Mode |
P |
Q |
R |
FREQ |
|
1 |
1 |
0 |
0 |
37.5 |
|
2 |
0 |
1 |
0 |
57.7 |
|
3 |
0 |
0 |
1 |
67.8 |
|
4 |
1 |
1 |
0 |
68.8 |
|
5 |
2 |
0 |
0 |
74.9 |
|
6 |
1 |
0 |
1 |
77.5 |
|
7 |
0 |
1 |
1 |
89.0 |
|
8 |
2 |
1 |
0 |
94.5 |
|
9 |
1 |
1 |
1 |
96.6 |
|
10 |
2 |
0 |
1 |
101.1 |
|
11 |
3 |
0 |
0 |
112.4 |
|
12 |
0 |
2 |
0 |
115.3 |
|
13 |
2 |
1 |
1 |
116.4 |
|
14 |
1 |
2 |
0 |
121.2 |
|
15 |
3 |
1 |
0 |
126.3 |
|
16 |
3 |
0 |
1 |
131.3 |
|
17 |
0 |
2 |
1 |
133.8 |
|
18 |
0 |
0 |
2 |
135.7 |
|
19 |
2 |
2 |
0 |
137.5 |
|
20 |
1 |
2 |
1 |
138.9 |
|
21 |
3 |
1 |
1 |
143.4 |
|
22 |
0 |
1 |
2 |
147.4 |
|
23 |
4 |
0 |
0 |
149.9 |
|
24 |
1 |
1 |
2 |
152.1 |
|
25 |
2 |
2 |
1 |
153.3 |
|
26 |
2 |
0 |
2 |
155.0 |
From 90hz up, this room is relatively smooth, but there's a hole in the support between 77 and 89 hz with a cluster around 70. Those 70hz notes really boom out, so I'm going to have to find something absorptive in that region.