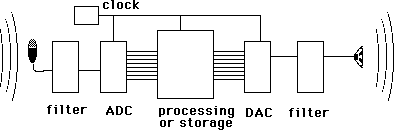
In a digital recording system, sound is stored and manipulated as a stream of discrete numbers, each number representing the air pressure at a particular time. The numbers are generated by a microphone connected to a circuit called an ANALOG TO DIGITAL CONVERTER, or ADC. Each number is called a SAMPLE, and the number of samples taken per second is the SAMPLE RATE. Ultimately, the numbers will be converted back into sound by a DIGITAL TO ANALOG CONVERTER or DAC, connected to a loudspeaker.

Fig. 1 The digital signal chain
Figure 1 shows the components of a digital system. Notice that the output of the ADC and the input of the DAC consists of a bundle of wires. These wires carry the numbers that are the result of the analog to digital conversion. The numbers are in the binary number system in which only two characters are used, 1 and 0. (The circuitry is actually built around switches which are either on or off.) The value of a character depends on its place in the number, just as in the familiar decimal system. Here are a few equivalents:
BINARY DECIMAL
0=0
1=1
10=2
11=3
100=4
1111=15
1111111111111111=65535
Each digit in a number is called a BIT, so that last number is sixteen bits long in its binary form. If we wrote the second number as 0000000000000001, it would be sixteen bits long and have a value of 1.
The number of bits in the number has a direct bearing on the fidelity of the signal. Figure 2 illustrates how this works. The number of possible voltage levels at the output is simply the number of values that may be represented by the largest possible number (no "in between" values are allowed). If there were only one bit in the number, the ultimate output would be a pulse wave with a fixed amplitude and more or less the frequency of the input signal. If there are more bits in the number the waveform is more accurately traced, because each added bit doubles the number of possible values. The distortion is roughly the percentage that the least significant bit represents out of the average value. Distortion in digital systems increases as signal levels decrease, which is the opposite of the behavior of analog systems.
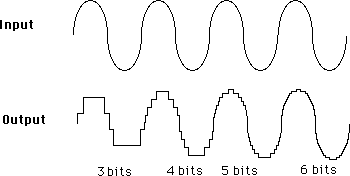
Fig. 2 Effect of word size
The number of bits in the number also determines the dynamic range. Moving a binary number one space to the left multiplies the value by two (just as moving a decimal number one space to the left multiplies the value by ten), so each bit doubles the voltage that may be represented. Doubling the voltage increases the power available by 6 dB, so we can see the dynamic range available is about the number of bits times 6 dB.
The rate at which the numbers are generated is even more important than the number of bits used. Figure 3. illustrates this. If the sampling rate is lower than the frequency we are trying to capture, entire cycles will be missed, and the decoded result would be too low in frequency and might not resemble the proper waveform at all. This kind of mistake is called aliasing. If the sampling rate were exactly the frequency of the input, the result would be a straight line, because the same spot on the waveform would be measured each time. This can happen even if the sampling rate is twice the frequency of the input if the input is a sine or similar waveform. The sampling rate must be greater than twice the frequency measured for accurate results. (The mathematical statement of this is the Nyquist Theorem.) This implies that if we are dealing with sound, we should sample at least 40,000 times per second.
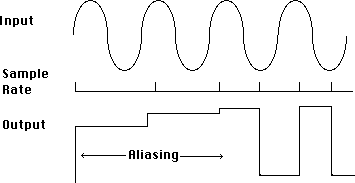
Fig. 3 Effects of low sample rates
The Nyquist rate (twice the frequency of interest) is the lowest allowable sampling rate. For best results, sampling rates twice or four times this should be used. Figure 4 shows how the waveform improves as the sampling rate is increased.
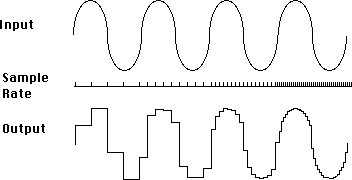
Fig. 4 Effect of increasing sample rate
Even at high sample rates, the output of the system is a series of steps. A Fourier analysis of this would show that everything belonging in the signal would be there along with a healthy dose of the sampling rate and its harmonics. The extra junk must be removed with a low pass filter that cuts off a little higher than the highest desired frequency. (An identical filter should be placed before the ADC to prevent aliasing of any unsuspected ultrasonic content, such as radio frequency interference.)
If the sampling rate is only twice the frequency of interest, the filters must have a very steep characteristic to allow proper frequency response and satisfactorily reject the sampling clock. Such filters are difficult and expensive to build. Many systems now use a very high sample rate at the output in order to simplify the filters. The extra samples needed to produce a super high rate are interpolated from the recorded samples.
By the way, the circuits that generate the sample rate must be exceedingly accurate. Any difference between the sample rate used for recording and the rate used at playback will change the pitch of the music, just like an off speed analog tape. Also, any unsteadiness or jitter in the sample clock will distort the signal as it is being converted from or to analog form.
Once the waveform is faithfully transformed into bits, it is not easy to record. The major problem is finding a scheme that will record the bits fast enough. If we sample at 44,100 hz, with a sixteen bit word size, in stereo, we have to accommodate 1,411,200 bits per second. This seems like a lot, but it is within the capabilities of techniques developed for video recording. (In fact, the first digital audio systems were built around VCRs. 44.1 khz was chosen as a sample rate because it worked well with them.)
To record on tape, a very high speed is required to keep the wavelength of a bit at manageable dimensions. This is accomplished by moving the head as well as the tape, resulting in a series of short tracks across the tape at a diagonal.
On a Compact Disc, the bits are microscopic pits burned into the plastic by a laser.The stream of pits spirals just like the groove on a record, but is played from the inside out.To read the data, light from a gentler laser is reflected off the surface of the plastic (from the back: the plastic is clear.) into a light detector. The pits disrupt this reflection and yield up the data.
In either case, the process is helped by avoiding numbers that are hard to detect, like 00001000. That example is difficult because it will give just a single very short electrical spike. If some numbers are unusable, a larger maximum (more bits) must be available to allow recording the entire set. On tape, twenty bits are used to record each sixteen bit sample, on CDs, twenty-eight bits are used.
Even with these techniques, the bits are going to be physically very small, and it must be assumed that some will be lost in the process. A single bit can be very important (suppose it represents the sign of a large number!), so there has to be a way of recovering lost data. Error correction is really two problems; how to detect an error, and what to do about it.
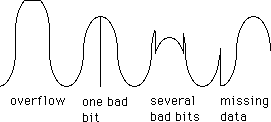
Fig. 5 Effects of data errors
The most common error detection method is parity computation. An extra bit is added to each number which indicates whether the number is even or odd. When the data is read off the tape, if the parity bit is inappropriate, something has gone wrong. This works well enough for telephone conversations and the like, but does not detect serious errors very well.
In digital recording, large chunks of data are often wiped out by a tape dropout or a scratch on the disk. Catching these problems with parity would be a matter of luck. To help deal with large scale data loss, some mathematical computation is run on the numbers, and the result is merged with the data from time to time. This is known as a Cyclical Redundancy Check Code or CRCC. If a mistake turns up in this number, an error has occurred since the last correct CRCC was received.
Once an error is detected, the system must deal gracefully with the problem. To make this possible, the data is recorded in a complex order. Instead of word two following word one, as you might expect, the data is interleaved, following a pattern like:
words 1,5,9,13,17,21,25,29,2,6,10,14,18,22,26,30,3,7,15,19,27 etc.
With this scheme, you could lose eight words, but they would represent several isolated parts of the data stream, rather than a large continuous chunk of waveform. When a CRC indicates a problem, the signal can be fixed. For minor errors, the CRCC can be used to replace the missing numbers exactly. If the problem is more extensive, the system can use the previous and following words to reconstruct a passable imitation of the missing one. One of the factors that makes up the price difference in various digital systems is the sophistication available to reconstruct missing data.
You may be wondering about the point of all of this, if it turns out that a digital system is more complex than the equivalent analog circuit. Digital circuits are complex, but very few of the components must be precise; most of the circuitry merely responds to the presence or absence of current. Improving performance is usually only a matter of increasing the word size or the sample rate, which is achieved by duplicating elements of the circuit. It is possible to build analog circuits that match digital performance levels, but they are very expensive and require constant maintenance. The bottom line is that good digital systems are cheaper than good analog systems.
Digital devices usually require less maintenance than analog equipment. The electrical characteristics of most circuit elements change with time and temperature, and minor changes slowly degrade the performance of analog circuits. Digital components either work or don't, and it is much easier to find a chip that has failed entirely than one that is merely 10% off spec. Many analog systems are mechanical in nature, and simple wear can soon cause problems. Digital systems have few moving parts, and such parts are usually designed so that a little vibration or speed variation is not important.
In addition, digitally encoded information is more durable than analog information, again because circuits are responding only to the presence or absence of something rather than to the precise characteristics of anything. As you have seen, it is possible to design digital systems so that they can actually reconstruct missing or incorrect data. You can hear every little imperfection on an LP, but minor damage is not audible with a CD.
The aspect of digital sound that is most exciting to the electronic musician is that any numbers can be converted into sound, whether they originated at a microphone or not. This opens up the possibility of creating sounds that have never existed before, and of controlling those sounds with a precision that is simply not possible with any other technique.
For further study, I recommend Principles of Digital Audio by Ken C Pohlmann, published by McGraw-Hill inc ISBN number0-07-050469-5.
Peter Elsea 1996