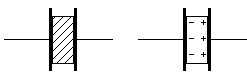
Ohm's law describes the relationship between current and voltage in circuits that are in equilibrium- that is, when the current and voltage are not changing. When we have a situation where the current changes (often called an AC circuit) more factors have to be taken into account.
There are devices that oppose any change in current flow. They are not noticed until the voltage changes, but when it does, these gadgets show some surprising properties, soaking up current and giving it back later, so that Ohm's law calculations come out wrong. The property of opposing change is called reactance. It is also measured in ohms.
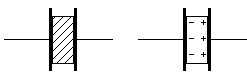
If you make a sandwich out of two metal plates and a piece of glass, you have made a capacitor. If you apply a positive voltage to one plate and a negative voltage to the other, current will flow for a while because the glass can store some electrons. This will stop eventually, as the glass absorbs as many electrons as it can. At this point we say the capacitor is fully charged, and a voltmeter connected between the two plates would show a reading close to that of whatever originally provided the current. If you then connect the two metal plates together, current will flow the opposite direction as the capacitor discharges.
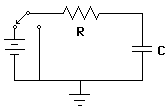
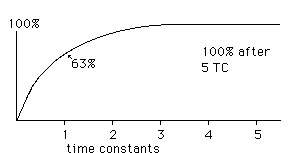
The current flow is not steady throughout this process. Starting from the discharged stage, current flows strongly at first, but slows down as the voltage across the capacitor approaches the charging voltage. Likewise, when discharged, current flows strongly at first, then tapers off as the charge approaches zero. Any resistance between the charging source and the discharged capacitor will limit the initial charging current- as the capacitor charges the voltage across the resistor is reduced (it's the difference between the voltage source and the rising voltage of the capacitor plate.) The resistor obeys ohm's law, so the current into the capacitor ( and apparently out the other side) dwindles in the gradual curve shown here:
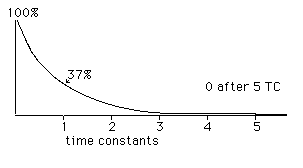
Current as capacitor charges
This means the voltage across the capacitor changes in a curve too:
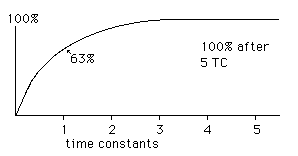
Voltage across capacitor as it charges.
The time it takes this to happen is determined by the resistance the current must pass through and the size and material of the capacitor. Since it changes very slowly at the end, it is impossible to find the time the capacitor is 100% charged. In fact it never really gets there. A "time constant" is defined as the time it takes to get to 63% of full charge. A value for measuring the size of the capacitor (called capacitance) is then defined by the formula
![]()
Capacitance is measured in "farads", and a one farad capacitor in series with a one ohm resistor has a time constant of one second. In real life, we deal with large resistances and pretty short times, so the capacitors in most circuits have values in the microfarad range. (That's 10-6 farad.)
If you connect two capacitors in parallel, you make a bigger capacitor, and their values add:
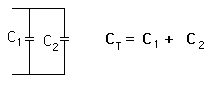
If they are connected in series, you get this:
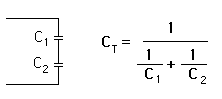
AC and the capacitor
Now imagine charging and discharging the capacitor very quickly- we could do this by using a tone generator instead of a battery as the voltage source.
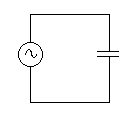
If we start with a high frequency and watch the current though the circuit, it's almost as if the capacitor weren't there at all! That's because the current is highest early in the charge cycle, and if the current source changes direction much faster than a time constant, it's always early in the charge cycle. If the frequency is reduced, the current amplitude decreases- to the point where there's nothing but a slight ripple in a steady value.
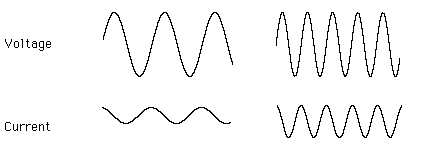
There's another important thing to notice here: the current is 90° out of phase with the voltage, the current leading.
As you can see, we have a situation where Ohm's law doesn't tell the entire story. The current through a capacitor is dependent on the frequency of the signal. Frequency dependent opposition to current is reactance, which is indicated in formulas by the letter X. Capacitive reactance is found with the formula:
X is reactance in ohms.
F is frequency in hertz.
C is capacitance in farads.
Since the frequency term is in the bottom of the fraction, you can see that as the frequency falls, the reactance goes up. In other words, capacitors impede low frequency signals.
Combining capacitive reactance and resistance
To make Ohm's law work for changing currents, we redefine it as
I=E/Z
Where Z represents impedance, the
opposition to all current, changing or not. The impedance of a
resistor and capacitor in series is found by the formula:![]()
The impedance of a resistor and capacitor in parallel is a bit more complex:
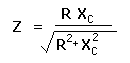
A Simple Filter
A resistor and a capacitor can be combined to make an AC current divider or filter circuit.
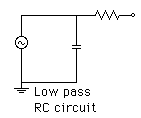
When the frequency is low, the impedance of the capacitor is high, so most current will flow through the resistor. As the frequency increases, more current is diverted through the capacitor, less to the rest of the circuit. Thus, the response is low pass. If you exchanged the capacitor and resistor, you'd have a high pass circuit.
The cutoff frequency is defined as the frequency for which the resistance of the resistor equals the reactance of the capacitor. At that point, the signal is .707 times the original amplitude or reduced by 3db. Above the cutoff frequency, the signal falls by 6db per octave. Below that point (in the passband) the signal is unaffected. To find the cutoff frequency:
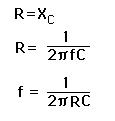
Inductors
Capacitors are not the only gadgets that have reactance. If you take some wire and coil it tightly, you have made an inductor. This is what happens:
 When current passes through the
inductor L, a magnetic field is generated. It doesn't appear
suddenly, it builds up. A magnetic field moving past a wire generates
current, and a growing field is moving. In this case, it's moving
past the wires of the coil itself in such a way as to oppose the
incoming current, so the current flow is delayed like this:
When current passes through the
inductor L, a magnetic field is generated. It doesn't appear
suddenly, it builds up. A magnetic field moving past a wire generates
current, and a growing field is moving. In this case, it's moving
past the wires of the coil itself in such a way as to oppose the
incoming current, so the current flow is delayed like this:
Look familiar? It's the same sort of curve as the capacitor, except the current through an inductor builds like the voltage across a capacitor. (And yes, the voltage across the inductor starts high and falls, like current into a capacitor.) What I really find fascinating about inductors is that after the current source is removed, the collapsing magnetic field keeps the current going for a bit.
In many ways, an inductor is the opposite of a
capacitor. It has a time constant:![]()
Where L is the inductance in units called henrys. The inductance for inductors in series and parallel follows the form for resistors, at least if the inductors aren't close enough together to interact magnetically.
The reactance of an inductor is:
![]()
Since the frequency is just multiplied by the inductance, inductors impede high frequency signals. When you apply a sine wave to an inductor, the current lags behind the voltage by 90°.
You can make filters with resistors and inductors, but they aren't common in audio because inductors of the appropriate size are fairly large. Radio and video circuits use them a lot.
Inductors and capacitors combined
When you place an inductor in series with a capacitor, you get an interesting effect. The impedance is found by:
![]()
The impedance is the absolute value of the difference of the reactance of the capacitor and inductor. Since the signal frequency is used to compute both reactance parts but one is rising with frequency and one is falling, the impedance curve looks like this:
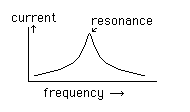
There is a magic frequency, called the resonance frequency, where plenty of current flows, but above and below resonance, there is less current. If the capacitor and the inductor are in parallel, this formula gives the impedance:
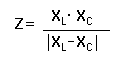
The current verses frequency plot looks like this:
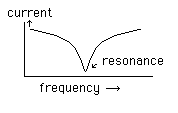
What's going on here? Well, at low frequencies, the inductor passes pretty much everything (remember, an inductor is just a wire for DC) and the capacitor blocks everything. As the frequency rises, the inductor impedes, but the capacitor will take over. When the impedances of both match, you get no current flow. How is this possible?
It's because of the phase changes: the current through a capacitor is 90° ahead of the voltage, and the current through the inductor is 90° behind. When the circuit is in resonance, the two cancel out. In real circuits, series resistance tends to reduce the peaks. This is called damping, and the ratio of inductive reactance to resistance is known as Q (for quality factor).
Transformers
As I mentioned before, you don't see a lot of inductors in audio circuits, primarily because of size, but also because they aren't very precise compared to capacitors. There is one vital function that only inductors can do well:
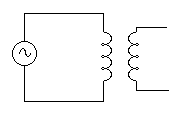
If two inductors are close together, current flowing in one will induce current in the other. Such an arrangement is called a transformer. As far as audio goes, there are three useful features of transformers:
So, we use transformers for isolation, noise rejection, and changing voltage of AC signals (most often to adjust the mains power to something useful for audio circuitry.) We'll mention them again. Just remember that transformers are inductors first and have all of the impedance and frequency effects we have just discussed.
pqe 10/1/98