
You have noticed many objects have a tendency to return to their original location after they have been moved slightly. You have probably also noticed most objects not only return to their original position but continue too far, so that they may swing back and forth several times before they come to rest. A playground swing is a convienent example for a discussion of this kind of motion, because we have all ridden one, and more importantly, pushed one.

Fig. 1 Motion of a swing
If given one strong push, a swing will move back and forth because the earth's gravity is pulling down while the rope is making the swing move in a partial circle. When the swing has returned to the starting point, it can't go down any more, but still has a lot of momentum to use up, so it moves beyond the center and up on the other side until gravity slows it down and pulls it back to the center, but it still has too much momentum.. and so forth. This whole operation is periodic: each complete swing takes the same amount of time, regardless of how far the swing moves. When the arc of swing is large, the swing moves quickly, when the arc is small, the swing moves slowly. The amount of time it takes the swing to complete its cycle depends on the length of the rope and nothing else. If you make a graph of the distance the swing travels crossways with time, the result is a sine wave.
The only thing slowing the swing down is friction with the air and within the rope. If you were to replace the energy lost to this friction, you could keep the swing going forever. If you try this by giving the swing extra pushes, you very quickly discover you must push at the right time and in the right direction, or you waste your push or perhaps slow the swing down. Specificaly, the time between pushes must correspond with the period of the swing, and you must push in the same direction the swing is already going.
Now there are many objects that behave like swings in their motion (In classical physics this behavior is termed SIMPLE HARMONIC MOTION). In fact, any object that is even slightly movable, has mass, and has some tendency to return home when disturbed will do this. Sound waves can contribute to the simple harmonic motion of an object if the period of the wave and period of the motion of the object are about the same. This phenomenon is called RESONANCE. In the next essay you will see that resonance is an important factor in the operation of acoustic musical instruments.
One harmonic motion machine that is particularly interesting is an ordinary pop bottle.
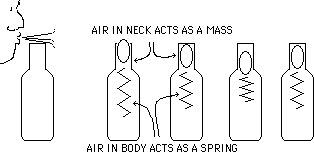
Fig. 2 Harmonic motion in a bottle.
When you blow across the bottle opening, the air in the neck behaves as a mass on the end of a spring. (The air in the body of the bottle is the spring.) The flow of air across the top pulls the neck mass a little bit out of the bottle, which reduces the pressure within the body. That low pressure pulls the neck mass back in, and the result is an oscillation of the air in the neck. The rate of oscillation is determined by the mass of the air in the neck and the size of the body of the bottle. This system is resonant enough that it will respond to any sort of air disturbance with some oscillations at its characteristic frequency. Helmholtz used bottles in this way when he proved that complex sounds contained a mix of partials of various frequencies.
Peter Elsea 1996