It is adequate for a music class to take a rather simplistic view of the precise nature of electricity, so the following discussion is not complete or rigorous.
The phenomenon known as electricity involves the exchange of very small particles (electrons) between atoms. Now a particular atom generally possesses a constant number of electrons, and there are some rather potent forces within the atom working to keep the correct number of electrons, so if an atom looses an electron because of some mechanical or chemical process, it will very quickly pull in a replacement. There are seldom spare electrons around, so the replacement likely comes from an adjacent atom, which, shy one electron, steals from its neighbor, and so forth. The exchange of electrons propagates in much the same way as the pressure disturbance I discussed in the section on sound, and exhibits all of the associated wave effects. The speed of propagation is so high however, (almost the speed of light) that we may ignore the wave characteristics of electricity for all but the briefest events.
The electron exchange has two important side effects: it produces a tiny amount of heat or light, and supports a weak magnetic field. These two effects represent an energy loss, and must be compensated for by the original electron moving mechanism. They can also be thought of as energy transference from the point of generation to any place where these effects are apparent. Most of the science of electrical engineering deals with getting these effects to happen at the right place.
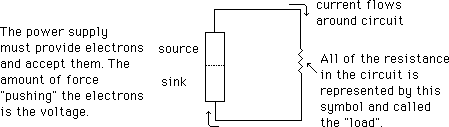
Since the heat and magnetism effects are small, in order to produce any useful work we must move a lot of electrons and ensure that it is a continuous process. To get a steady flow of electricity, we must have something that absorbs electrons (called a sink) something that supplies electrons (a source), and some path in between for the electrons to follow. If we want the process to be continuous forever, we must realize the sink will eventually fill and the source will be depleted, so the two should be combined and the path from one to another be made circular. The source/sink combination can be realized chemically with a battery or mechanically with a generator, or in a variety of ways I'll lump together and call the power supply.
VOLTAGE, CURRENT, RESISTANCE
If we set up a power supply and a wire connecting its source and sink terminals, we can make some observations about the flow of electricity in this simple circle, or circuit.

Fig. 1 A simple circuit.
The amount of heat or light produced is determined by the number of electrons moving around. The concept of "number of electrons" is called CURRENT and is measured in units called AMPERES. The symbol used to stand in for current in mathematical formulas is I.
The amount of heat produced for a given current depends on the material used for the wire. The heat producing mechanism opposes the flow of electrons, so it is termed the RESISTANCE. It is measured in units called OHMS, and the symbol is R. Many materials have such a high resistance that they will not carry measurable current. Such materials are termed insulators, whereas materials that will carry current are conductors.
If you want to move a current against a resistance, you must supply some ELECTROMOTIVE FORCE. This force is measured in VOLTS, is symbolized by V or E, and is a property of the power supply or battery. Electromotive force is a bit of a mouthfull, so it is also called VOLTAGE. Since this force acts in moving current from one spot to another (from source to sink) a voltage measurement must be made between two places. If the two places are on the same piece of wire, the voltage will be unmeasurable. Usually, we designate a convenient spot as being "0 volts" and use that as a common point in all measurements.
These three properties are everything we need to know about a constant current flow. They are related in the following way:
If the voltage is held constant, and the resistance reduced, the current will increase.
If the resistance is not changed, but the voltage is reduced the current will decrease.
If we know two of the quantities, we can calculate the third, because the units are defined that way.
The mathematical statement of these relationships is:
I=E/R
Where (to review),
I is current in Amperes,
Eis electromotive force in Volts, and
R is resistance in Ohms.
This relationship is the cornerstone of electronics, and is known as OHM'S LAW.
There are many uses for current flow, of course. In fact, our modern civilization is pretty dependent on it. The two most important are the transmission of power and the transmission of information. In electronic music, we use electricity mostly to transmit and modify information; the flow of current represents the pressure of air as it changes to produce sound. To do this, we use devices that generate current from the energy of the sound waves, and ultimately, devices that generate sound from changes in current.
IMPEDANCE
Ohm's law is true for any steady state condition but if the current is changed, Ohm's law is not true while the change is taking place. This is because there are effects that oppose any change in the amount of current flow. Opposition to current change is called REACTANCE, and is measured in ohms because it must be combined with resistance in order to describe the current to voltage relationship. (For the time being, think of reactance as the electrical equivalent of momentum.)
This combination is not a simple addition because it must take into account the rate of change. The rate correction is usually computed on the basis of frequency of a sine wave. Some structures have a reactance which increases with frequency, and some devices have a reactance that decreases as frequency rises. There are complex devices that favor certain frequency regions but react against frequency content above or below the magic value. The combination of resistance and reactance is called IMPEDANCE (symbolized by Z).
Ohm's law for impedance is stated:
I=E/Z
Where I= the current amplitude of the signal[*]
E= the voltage amplitude of the signal*
Z= the impedance of the circuit at the frequency of the signal.
The moral of all this is that for a given voltage, low impedance circuits require large currents, and high impedance circuits require small currents.
POWER
There is little point in moving these electrons around unless the current can make something happen. How much can happen is expressed by the POWER of the circuit. In a resistive circuit (i.e. no reactance in any of the components) the power is the product of the voltage and the current, and is expressed in watts.
P=EI
For instance, a light bulb that passes a half ampere of current if one hundred volts is applied to it will produce 50 watts worth of light and heat. If the bulb were redesigned to pass a whole ampere, it would provide 100 watts. If 200 volts were applied to the original bulb, it would also provide 100 watts, but probably not for long.
Power calculations in reactive or partially reactive circuits are complex. The ratings on light bulbs and appliances assume you are going to use the resistive power formula to determine whether a fuse will blow, even if the device is reactive. (In the latter case the label should read VA for volt-amperes instead of W for watts.)
INFORMATION
When electricity is used to transmit information, we lose interest in voltage and current values (as long as there is enough of both for the circuit to work) and pay attention to how much information can be represented in a second and how accurate that representation is. We use two basic systems to represent information. In analog systems, the amount of current varies directly with the represented quantity, such as air pressure. In digital systems, the information is coded into binary numbers, and the value of each bit of the number is represented by the presence or absence of current.
For analog systems, the accuracy of representation is measured as percent of distortion; which is the difference between whatever went into the system and the actual output compared to the "perfect" output. The amount of information that may be represented is termed the bandwidth. For instance, a high fidelity sound system that can reproduce sound from 20hz to 20,000hz has a bandwidth of 19980hz.
In digital systems, the amount of information is determined by the number of bits that may be transmitted per second, also known as the baud rate. The accuracy is the percentage of bits that are transmitted wrong or the error rate. Translation of baud rate to bandwidth and error rate to distortion is a function of the encoding scheme used; some are fast and sloppy, others are accurate and slow. Low distortion, high bandwidth data transmission is expensive no matter what system is used.
In both analog and digital audio systems, the representation of sound is usually called the signal. We will often trace the signal path through various devices, which, because they modify the information, are called signal processors. Any output the system produces which is not the signal is considered noise.
Peter Elsea 1996